Given a square grid of size N, each cell of which contains integer cost which represents a cost to traverse through that cell, we need to find a path from top left cell to bottom right cell by which the total cost incurred is minimum. From the cell (i,j) we can go (i,j-1), (i, j+1), (i-1, j), (i+1, j). Note: It is assumed that negative cost cycles do not exist in the input matrix. Minimum Cost For Tickets. 2636 49 Add to List Share. In a country popular for train travel, you have planned some train travelling one year in advance. The days of the year that you will travel is given as an array days. Each day is an integer from 1 to 365. The minimum efficient scale (MES) is the lowest point on a cost curve at which a company can produce its product at a competitive price. At the MES point, the company can achieve the economies of. To get the maximum value, use the MAX function. MAX takes one or arguments, each representing a number or range or numbers. In this case, we just need to supply the named range prices. To get the minimum price in this list, we need to use the MIN function.

Definition: The Least Cost Method is another method used to obtain the initial feasible solution for the transportation problem. Here, the allocation begins with the cell which has the minimum cost. The lower cost cells are chosen over the higher-cost cell with the objective to have the least cost of transportation.

Mac software download for sandisk ultra plus 64gb. The Least Cost Method is considered to produce more optimal results than the North-west Corner because it considers the shipping cost while making the allocation, whereas the North-West corner method only considers the availability and supply requirement and allocation begin with the extreme left corner, irrespective of the shipping cost.

Let’s understand the concept of Least Cost method through a problem given below:

In the given matrix, the supply of each source A, B, C is given Viz. 50units, 40 units, and 60 units respectively. The weekly demand for three retailers D, E, F i.e. 20 units, 95 units and 35 units is given respectively. The shipping cost is given for all the routes.

The minimum transportation cost can be obtained by following the steps given below:

1. The minimum cost in the matrix is Rs 3, but there is a tie in the cell BF, and CD, now the question arises in which cell we shall allocate. Generally, the cost where maximum quantity can be assigned should be chosen to obtain the better initial solution. Therefore, 35 units shall be assigned to the cell BF. With this, the demand for retailer F gets fulfilled, and only 5 units are left with the source B.
2. Again the minimum cost in the matrix is Rs 3. Therefore, 20 units shall be assigned to the cell CD. With this, the demand of retailer D gets fulfilled. Only 40 units are left with the source C.
3. The next minimum cost is Rs 4, but however, the demand for F is completed, we will move to the next minimum cost which is 5. Again, the demand of D is completed. The next minimum cost is 6, and there is a tie between three cells. But however, no units can be assigned to the cells BD and CF as the demand for both the retailers D and F are saturated. So, we shall assign 5 units to Cell BE. With this, the supply of source B gets saturated.
4. The next minimum cost is 8, assign 50 units to the cell AE. The supply of source A gets saturated.
5. The next minimum cost is Rs 9; we shall assign 40 units to the cell CE. With his both the demand and supply of all the sources and origins gets saturated.

The total cost can be calculated by multiplying the assigned quantity with the concerned cost of the cell. Therefore,

Total Cost = 50*8 + 5*6 + 35*3 +20*3 +40*9 = Rs 955.

Note: The supply and demand should be equal and in case supply are more, the dummy source is added in the table with demand being equal to the difference between supply and demand, and the cost remains zero. Similarly, in case the demand is more than supply, then dummy destination or origin is added to the table with the supply equal to the difference in quantity demanded and supplied and the cost being zero.

The min cost flow problem

Closely related to the max flow problem is the minimum cost (min cost) flow problem, in which each arc in the graph has a unit cost for transporting material across it. The problem is to find a flow with the least total cost.

The min cost flow problem also has special nodes, called supply nodes or demand nodes, which are similar to the source and sink in the max flow problem. Material is transported from supply nodes to demand nodes.

• At a supply node, a positive amount — the supply — is added to the flow. A supply could represent production at that node, for example.
• At a demand node, a negative amount — the demand — is taken away from the flow. A demand could represent consumption at that node, for example.

For convenience, we'll assume that all nodes, other than supply or demand nodes, have zero supply (and demand).

For the min cost flow problem, we have the following flow conservation rule, which takes the supplies and demands into account:

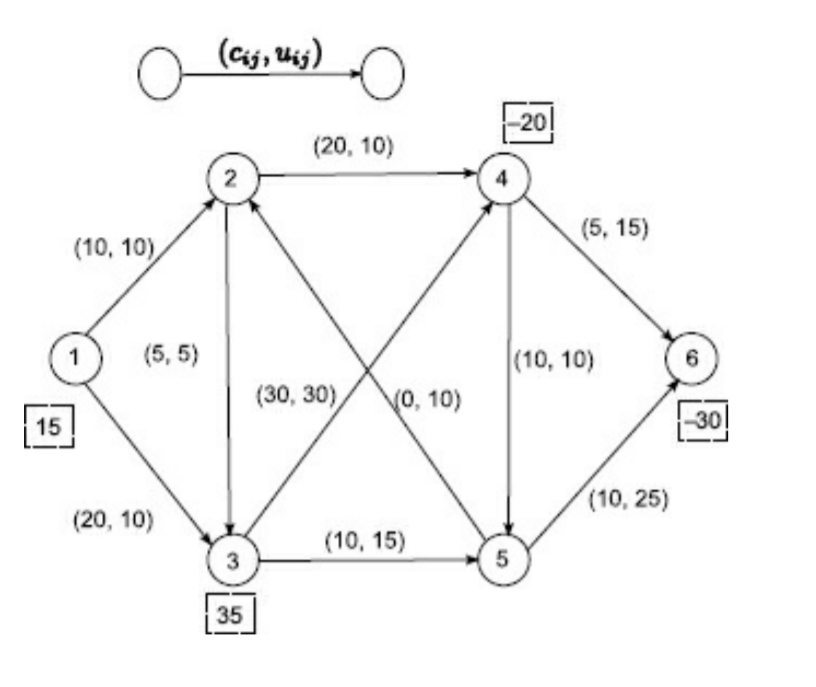
At each node, the total flow leading out of the node minus the total flow leading in to the node equals the supply (or demand) at that node.

The graph below shows a min cost flow problem. The arcs are labeled with pairs of numbers: the first number is the capacity and the second number is the cost. The numbers in parentheses next to the nodes represent supplies or demands. Node 0 is a supply node with supply 20, while nodes 3 and 4 are demand nodes, with demands -5 and -15, respectively.

Define the data

The following code defines the data for the problem. In this case, there are four arrays for the start nodes, end nodes, capacities, and unit costs. Again, the length of the arrays is the number of arcs in the graph.

Declare the solver and add the arcs

Minimum Cost To Open A Roth Ira

To solve the problem, we use the SimpleMinCostFlow solver. (The C# name for the solver is MinCostFlow.)

For each start node and end node, we create an arc from start node to end node with the given capacity and unit cost, using the method AddArcWithCapacityAndUnitCost.

The solver's SetNodeSupply method creates a vector of supplies for the nodes.

Invoke the solver and display the results

Now that all the arcs have been defined, all that remains is to invoke the solver and display the results. We invoke the Solve() method, and then display the flow and cost across each arc.

Minimum Cost To Connect Sticks

Here is the output of the Python program:

Complete programs

Minimum Cost Equation

Putting it all together, here are the complete programs in Python and C#.

SimpleMinCostFlow methods

Download flash movie player for mac. The SimpleMinCostFlow Flow class provides the following methods, most of which are not used in the preceding example:

Least Cost Method Transportation Model

• AddArcWithCapacityAndUnitCost()
• SetNodeSupply()
• Head()
• NumArcs()
• NumNodes()
• MaximumFlow()
• OptimalCost()
• Solve()
• SolveMaxFlowWithMinCost()
• Tail()

More detail on each of these is available in the SimpleMinCostFlow reference page.